Anyway, today I was privileged to sit in on several fantastic lessons but I really want to share this one with you.
Topic - Finding Volume of Irregular 3D Shapes
Link to Previous Learning:
The class had been looking previously at how to work out the volume of regular cubes and rectangular prisms. The teacher presented this diagram:
There was a brief discussion about this shape along the lines of how it was similar to and different from the previous shapes that the class had worked with. Everyone seemed happy with what they could see.
Problem Solving Strategies:
Then the teacher asked them for some strategies to deal with this shape.
Two students had ideas:
1. You can separate the shape into smaller parts
2. You can add different bits of the shape together
Even though expressed differently, I think both ideas showed that the kids were looking at the composition of the shape and demonstrated their knowledge of how smaller shapes can be combined to make bigger shapes. This is something that they had done previously in Year 4 with 2-dimensional shapes.
Working Independently:
The class quickly got down to work. To save time, the teacher had prepared multiple copies of the diagram, drawn to a scale of 1:1. This was really helpful - no time spent on doing activities that were not related to the topic. Yes - drawing shapes is a great skill to learn - but not in this lesson. The focus here was always going to be on finding the volume.
The teacher circulated and talked with different children. Once they had a solution, they were encouraged to get another copy of the diagram and work it out another way.
Presentation:
The teacher selected several children who had different strategies and asked them to prepare a presentation for the class. This involved getting some A3 paper with a copy of the diagram (already prepared by the teacher) to write up their solution.
Method 1:
A simple cut divides the shape into two manageable pieces. Works well and gets an accurate solution.
Note the use of colour in the diagram to highlight the relevant calculations. This was done by the teacher after the presentation when she was clarifying with the students what was going on.
Method 2:
In this solution, the student decided to chop off the top part and add it to the end of the remaining rectangular prism. This works neatly because the base of the chopped off part is 4cm x 6cm, same as the end of the bigger rectangular prism. Neat match!
There was some confusion and almost disbelief - some students wanted clarification on how this worked.
So the teacher pulled out a model of the shape to show them.
I think she was holding back on showing this model because she didn't want to shape the children's thinking. Personally, I think I might have got the model out earlier or at least got the kids to make the model for themselves BUT making models wasn't the point of the lesson - everything points back to the topic: "Finding the volume of irregular 3D shapes."
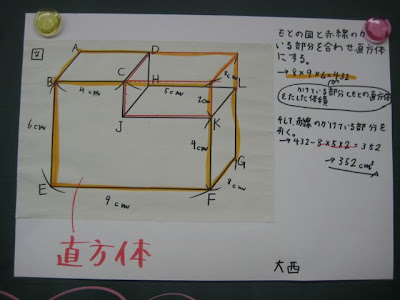
Method 3:
This method starts by working out the volume if there was no missing part and subtracting the piece that is gone. Notice once again the use of colour (by the teacher) to show which part of the calculation relates to which part of the diagram.
Same and Different:
This part of the conversation is always interesting.
The two things that children identified were:
1. You had to use multiplication
2. You had to find rectangular prisms
Generalisation:
"You can find these volumes by looking for cubes and rectangular prisms."
- a very rough translation from the Japanese
So the students now had a strategy to deal with similar problems. The focus wasn't on getting the number answer correct, in fact it was only peripheral to the conversation.
AND
THE WAS NO MENTION ANYWHERE OF A FORMULA.
I think this was pretty significant - that's why I put it in caps