A Peter Sullivan Puzzle
We had a visit a few years ago from Peter Sullivan, former president of AAMT and a really inspirational mathematician. He showed us a puzzle that was like a 100 square cut into pieces like a jigsaw but the numbers were from 100 to 8000, counting up by 100s.
We were using them today as a bit of a fun challenge.
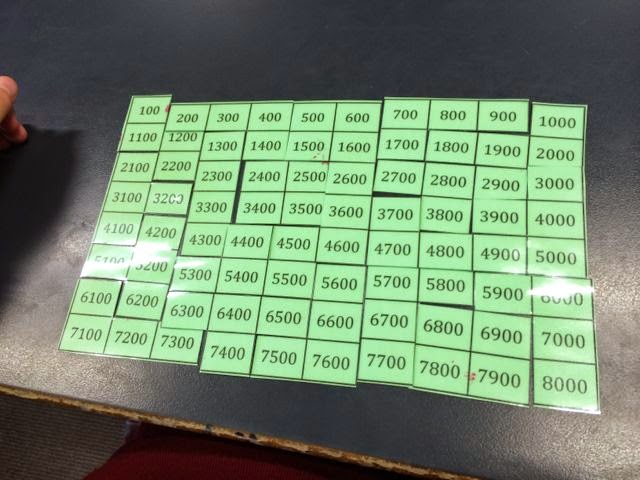
Here's what the finished puzzle looks like:
...and here's what it looks like when the kids start with it:
Bits everywhere and lots of disorganisation.
I had cut the pieces out differently for each puzzle - so looking at what your friend was doing was of little help.
I was really interested to see how the kids went about getting the puzzle back together again.
Here's a few examples:
Interestingly, none of the students went looking for the first square or the lowest number. They were able to complete the puzzle by just finding a few bits that went together and could work out the rest by going forwards, backwards, up and down from there.
So do I really need to get kids to solve puzzles and patterns by starting at the start? Why can't they start in the middle? Or at the end? Or...?
Time for me to reflect on some of my assumptions.
We were using them today as a bit of a fun challenge.
Here's what the finished puzzle looks like:
...and here's what it looks like when the kids start with it:
Bits everywhere and lots of disorganisation.
I had cut the pieces out differently for each puzzle - so looking at what your friend was doing was of little help.
I was really interested to see how the kids went about getting the puzzle back together again.
Here's a few examples:
This one started at the right because that was where he found his
first pieces that joined together.
This one started at the top - same reason. It was where the first
pieces fitted together.
And this one is almost finished but it's not particularly straight and...
hey! I think a piece is missing!
Oops! There it is on the floor!
Interestingly, none of the students went looking for the first square or the lowest number. They were able to complete the puzzle by just finding a few bits that went together and could work out the rest by going forwards, backwards, up and down from there.
So do I really need to get kids to solve puzzles and patterns by starting at the start? Why can't they start in the middle? Or at the end? Or...?
Time for me to reflect on some of my assumptions.
Me reflecting:
I wanted to use this pic - I saw it in a presentation this week. It's one of
those ones that pop up on Google searches.
Check out the cogs - is it really going to work if they spin
in the direction of the arrows???