It never gets boring because each day a new pattern, idea or interpretation emerges. This is the joy of inquiry in maths.
I had an idea a few nights ago that we tried out in class yesterday. Pictures are below.
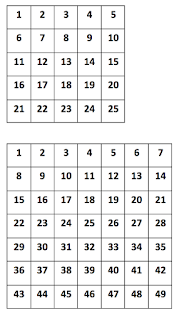
I was thinking about the 100's square and how kids see patterns in the numbers. Like skip counting, patterns in the units column, patterns in the tens column etc.
I wondered what would happen if they covered their number patterns with coloured blocks.
Then I wondered what would happen if the grid under the coloured blocks wasn't the standard 100's grid.
What if it was only the even numbers?
Or what if it was the counting by 3's pattern?
Or what if it was counting by 10's?
Or what if we didn't start counting at 0 or 1 but chose some other number as the starting point?
And what if there weren't 10 numbers in a row, but maybe 5 or 7 or ...?
(Yes - I am a wonderer)
So I banged out a set of different grids for the kids to explore.
Here are the grids I made:
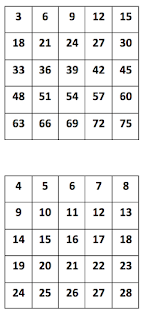
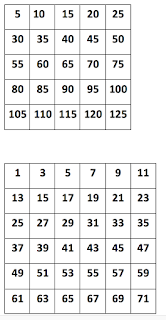
And then I asked the kids to look at any particular grid and find a pattern. Then I asked them to show their pattern by placing the coloured cubes on top of the numbers.
Finally I wondered if other people could work out what the numbers were underneath the cubes by looking at the pattern they made. And if they couldn't, would revealing a few of the numbers help give us a clue?
Here's what they did:
I made this pattern. Could you guess what numbers are underneath? What if I showed you a few of them?
Here's my pattern. It's actually a few patterns together. Let me show you one number. Any ideas?
What if I show you a few more numbers? Can you tell me what the patterns are?
This is two patterns put together. If I show you some of the red numbers, can you work out what the blue numbers are?
Does this help? And why have I put a red cube on top of a blue one in the fourth row?
"I am counting by 18. I just started with a different number for each colour cube."
(from an 8 year old - I was impressed.)
So have a look at this pattern. What do you see? What might the yellow numbers be? And the red ones? What would the next line look like?
Here are a few of the numbers uncovered. Can you work out what the other numbers on the grid would be?
Now I've taken away a few more. Does that help? Could you reconstruct the pattern and replace the missing cubes correctly?
This was a lot of fun. We had a lot of different things happening.
Next step will be to get the students to create their own grids to go under the cubes.
Or to create 3D grids.
Or to create grids that are not rectangular.
Or to....