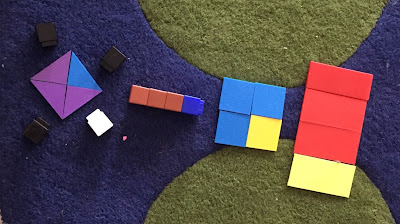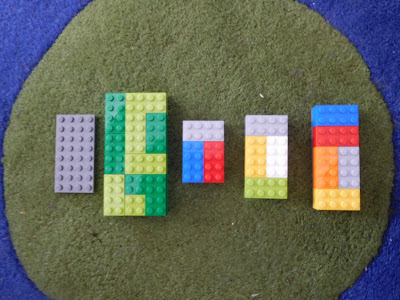Thursday 14 December 2017
Closing down for Christmas and Summer Hols
If you are wondering, I am on schools holidays until the first week in February.
Lots to look forward to next year:
- I'm back on Year 2 - yay!
- I will be doing some part time lecturing at ACU in Canberra
- I will be doing a lightning presentation at the SERC conference in Canberra
- I will be involved with presenting Maths300 workshops
- I hope to be playing bagpipes at the War Memorial on ANZAC Day
Let's see what happens.
Have a great holiday.
BF
Tuesday 21 November 2017
A Proportional Reasoning Sequence
This is a sequence that went over several days. I don't think we are finished (yet) but I wanted to get the initial stages written to clarify my thinking.
I was interested in looking at proportional reasoning. We had done a fair bit with fractions (halves, quarters etc). It was becoming obvious that we might benefit from some time looking at the relationships between the values of numbers and how we could represent this with size/length/area to make the relationship visual.
I have represented this sequence as "phases". They might be lessons. They might be something else.
Phase 1
I had a stack of coloured strips cut up.
The red strip is noticeably shorter (24cm) than the other colours (yellow, orange and green are all 29.5cm - the length of a piece of A4 paper). This was deliberate. I wanted the students to refer to the value they were certain of (red = 8) and use this as the basis of their reasoning, rather than simply fold each strip to the fraction of the whole.
eg if yellow = 4 (which is half of 8) then I might be tempted to just fold it in half without having to refer to the red unit at all.
After a time, two strategies emerged;
Strategy 1:
Some students decided that all the coloured strips needed to start off as the same length. Then they could fold yellow in half so it equalled 4; fold orange into quarters and then cut off one section to leave 3/4 because 6 = 3/4 of 8; then fold green into 8 parts and cut off 3 parts (5 = 5/8 of 8)
Strategy 2:
Other students folded the red strip into 8 equal parts and used this as a "ruler" to measure where to cut each of the other strips.
This was an interesting starting point. 8 was a good number because finding 4 and 6 was relatively easy but finding 5 required a bit more thinking.
Phase 2
And here are the strips I had prepared:
Look - he's done it again. Can't this guy cut the strips to even lengths?
No - I wanted to play with the kids' heads again. This time the purple strip (=24cm) was given a value of 6. How would you work out how long the other strips should be to show 1-5?
The kids pretty quickly realised they would have to find a way to divide the purple strip into 6 equal parts. Here is what happened:
Strategy 1:
Some students decided that a good way to find 6 equal parts was to fold the strip in half, then half again, then half again, making 8 equal parts. They then cut off two of the sections leaving 6 qual parts. This then became the measure showing where to cut the other strips.
Strategy 2:
Other students folded the purple strip into 3 parts using the z-fold technique. Then they folded this in half to make 6 equal parts.
Strategy 3
Not the most efficient strategy but totally effective, this student worked out how long a unit was, and then proceeded to cut out individual units in each colour and used these to establish the numbers 1-6.
What we found out
When we put these staircases into our 1cm grid books, we quickly found out that there was a number pattern. By counting how many squares high each step of the staircase was we found a counting-on pattern.
For students who used Strategy 1 or 3, the purple strip was 18cm long. They had started with 24cm then folded it into 8ths and then cut of 2/8 to make 6 equal parts. So their number pattern was the counting by 3's pattern.
For students who used Strategy 2, the pattern was the counting by 4's pattern, since 6 = 24cm, therefore 1 = 4cm.
Interestingly, no-one had considered using a ruler. They were busy exploring the relationships.
We also found out it was important to be accurate. In this picture (below) pink = 1 and blue = 5. But when they are put together, they are longer than the purple, which is meant to equal 6. This student has not fully understood the task. Their purple is folded into 8 sections. Their other units for 1-5 are a random series of increasing lengths.
At this point we paused and reflected on what we needed to do.
Phase 3
And so we moved to the next proposition. If you are given a unit (such as pink = 4) can you find the numbers less than and more than?
The students had made the Cuisenaire staircase hundreds of times. They quickly noticed that I had conveniently provided strips of paper using all 10 of the Cuisenaire colours.
This is the scene that greeted the kids when they came into the room.
They also noticed that the coloured strips were of varying sizes. Once again, I didn't want them to rely on any value other then pink = 4.
We were now showing that we understood the need to use pink = 4 as our basis for our reasoning about where to cut the other coloured strips.
There was much folding and cutting - and some even began to use additive strategies to find new numbers. For example, once I had calculated 2 and 3, I could work out 5 by putting them together. This showed me where I should cut the yellow for 5.
Some students used the white (=1) to add onto the end of their latest length to make the next length, showing that the number after n is n +1.
Some other students developed their own "ruler" once they had found the value of white = 1. They used this standard unit ruler to measure where to cut each strip.
And our friend from yesterday persisted with the strategy of cutting each colour into individual units and the glueing them into the book.
As I observed each of these events unfolding, I stopped the class and we had a moment of reflection to see what we could learn from each strategy.
Once we were done
After we had produced some nice looking staircases, I brought the class back together for another chat.
We had been thinking that pink = 4 all through this task.
But what if pink = 40?
Or 400?
Or 0.4?
Or 40%
Suddenly it all became clear - the model we had played with for half an hour was just a representation of a relationship based on proportion.
We could use reasoning to work out that...
- if pink = 40 then brown must be 80
- if pink = 400 then red must be 200
- if pink = 0.4 then blue must be 0.9 and orange must be 1.
"I think it should be 1.0," said one student. "We are talking decimals here you know."
Thursday 16 November 2017
Show me a quarter
I asked the kids to show me a quarter.
Here is what they did.
I'm not going to say anything.
Just I love those kids.
And yes, the yellow line has 3 squares,
which is a quarter of the total 12 squares used...
Friday 3 November 2017
Quarter of a Cross
There is a puzzle out there called "Quarter of a Cross". Amie Albrecht (@nomad_penguin) at the University of South Australia suggested that my Year 2 kids might like to give it a go. It is a puzzle that has appeal for learners from a range of ages. Amie had seen what we were doing with fractions last week and thought it would be interesting for my kids.
The puzzle looks like this:
So we gave it a go.
And here is what happened.
The first 10 minutes were spent coming to terms with the problem - what would a quarter look like?
Well we found lots of things that it wasn't. We soon realised that the cross could be made of five squares, so colouring in one or two of these was not going to make a quarter.
Back to the drawing board.
This was one of my favourite solutions because it showed me the struggle that was going on. It was like a window into the mind of the student.
"So, what if I do this? Hmm, no I don't think so. What about... yes that might work!"
It was the process of deciding on a "proof" - how to show I had found a quarter. Along the way, I am going to need to eliminate a few ideas but this is all part of the learning process.
While doing this task, I pulled the class back in for a "chat" about 3 times. This helped to clarify the question and also to discuss any important information we had discovered. This was shared with the class to help progress the solutions. We also had a break of a few hours and revisited the task in the afternoon.
And here are a few of the ideas that emerged:
1. You can use one of the "legs" of the cross and add it to 1/4 piece of the inside square.
What the students had seen was that 1/5 + 1/20 = 1/4 although they were not able to articulate this.
2. Using a line that passes through the centre of the cross
This was a good idea. If you extrapolate from this you will find that this method produces an infinite series of solutions as you rotate around the centre point. We only represented 3 solutions.
3. There is a left handed and a right handed house
Interesting - same idea but reflected.
4. Colour makes everything look good
So Amie - hope you like our pics. I think they look great. The kids had a really good time and it was difficult but we got some good learning out of it.
Now, I wonder what other shapes we could divide up...
The puzzle looks like this:
And here is what happened.
The first 10 minutes were spent coming to terms with the problem - what would a quarter look like?
Well we found lots of things that it wasn't. We soon realised that the cross could be made of five squares, so colouring in one or two of these was not going to make a quarter.
Back to the drawing board.
This was one of my favourite solutions because it showed me the struggle that was going on. It was like a window into the mind of the student.
"So, what if I do this? Hmm, no I don't think so. What about... yes that might work!"
It was the process of deciding on a "proof" - how to show I had found a quarter. Along the way, I am going to need to eliminate a few ideas but this is all part of the learning process.
While doing this task, I pulled the class back in for a "chat" about 3 times. This helped to clarify the question and also to discuss any important information we had discovered. This was shared with the class to help progress the solutions. We also had a break of a few hours and revisited the task in the afternoon.
And here are a few of the ideas that emerged:
1. You can use one of the "legs" of the cross and add it to 1/4 piece of the inside square.
What the students had seen was that 1/5 + 1/20 = 1/4 although they were not able to articulate this.
2. Using a line that passes through the centre of the cross
This was a good idea. If you extrapolate from this you will find that this method produces an infinite series of solutions as you rotate around the centre point. We only represented 3 solutions.
3. There is a left handed and a right handed house
Interesting - same idea but reflected.
4. Colour makes everything look good
So Amie - hope you like our pics. I think they look great. The kids had a really good time and it was difficult but we got some good learning out of it.
Now, I wonder what other shapes we could divide up...
Thursday 26 October 2017
Lego Fractions
We are continuing our exploration of fractions. I thought it might be interesting to see how we could represent unit fractions (1/2, 1/3, 1/4 etc) using one of our favourite learning tools - Lego!
So we started off gently. Let's have a look at 1/2...
Then 1/3...
Yep - that was pretty much what I was expecting.
So I asked, "Can you do it another way?"
Never fails...
Here is what 1/2 could look like:
Or this...
Or this...
And 1/3:
And...
And from that, a student worked out 1/1, 1/2, 1/3, 1/4, 1/5...
Yes, I know, we went beyond the Australian Curriculum requirements for Year 2 - but how do you stop the kids when they are on a roll and obviously know what they are doing?
Subscribe to:
Posts (Atom)